Adsorption of dendrimers on oppositely charged solid substrates
Since their synthesis by Vögtle and Tomalia in the eighties, dendrimers have developed into an very interesting class of novel polymeric materials. Potential applications include surface patterning, synthesis of nanoparticles, or gene delivery. Our research group was much involved in the study of adsorption of cationic dendrimers to negatively charged solid substrates, mainly silica, mica, or sulfate latex particles. This essay presents a summary of these results.
Polyamidoamine (PAMAM) dendrimers
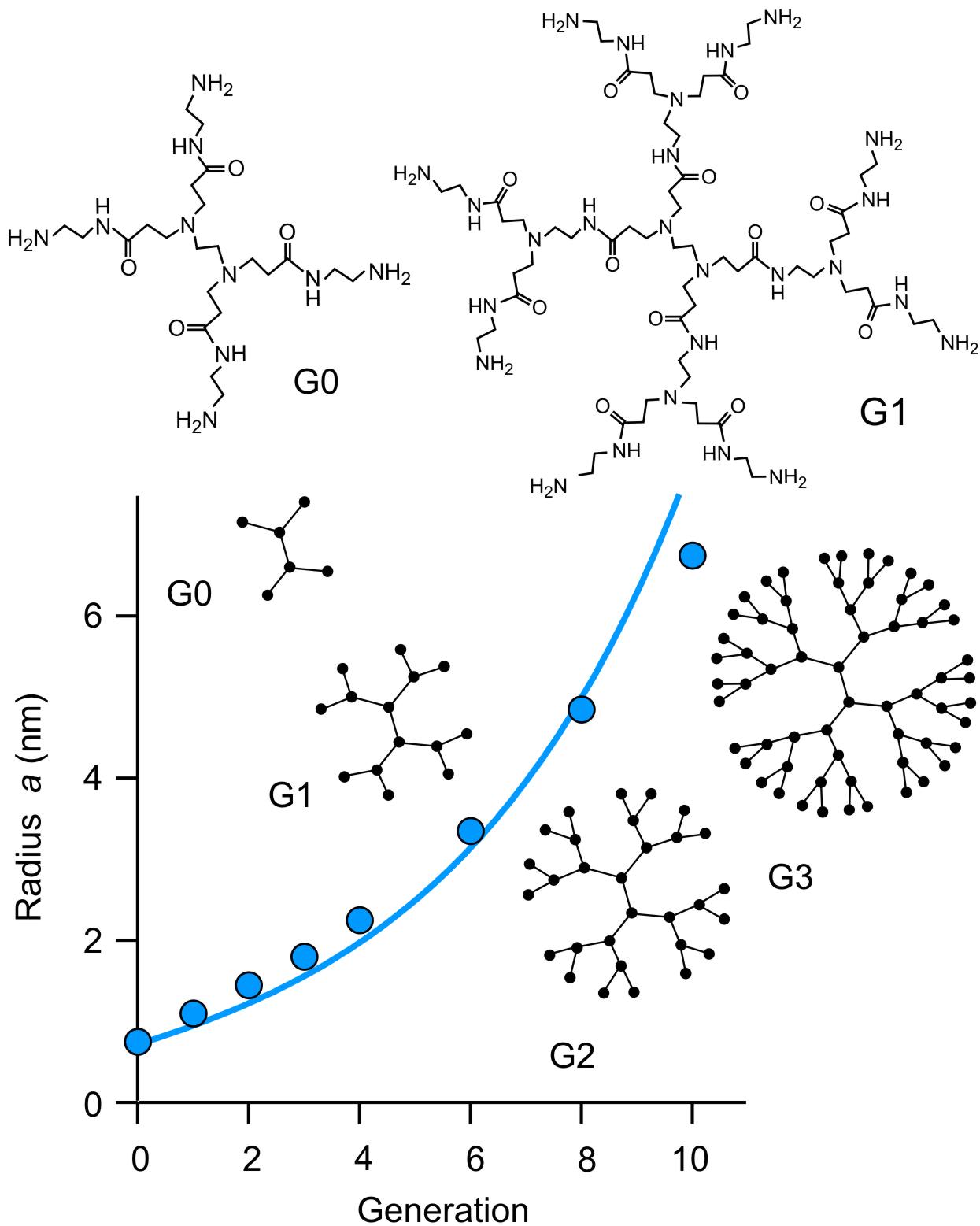
Dendrimers to be discussed are the commercially available polyamidoamine (PAMAM) dendrimers. Their chemical structure and architecture are illustrated in the right figure. They are synthesized in different generations, and each generation adds a corona of branching side groups. PAMAM dendrimers are available up to generation 10 (G10). The G10 dendrimer has a molecular mass of 935 kg/mol and radius in solution of about 7 nm. The dependence of their radius a can be described by the simple relation 4πa3/3 = vM/φ where v is the molecular volume of the monomer unit, M the molecular mass, and φ the volume fraction of the polymer. This relation assumes that the dendrimer can be approximated by a porous sphere containing water. In the experimental data of the hydrodynamic radii are shown in the lower part of the left figure and the solid line is the calculation based on the above relation with φ = 0.6. This model describes the data well, and one concludes that a dissolved PAMAM dendrimer consists of about half polymer and half water.
PAMAM dendrimers in solution may accumulate a substantial charge [2]. Since their charge originates from amine groups, they are almost neutral in basic conditions, and they become positively charged in acidic conditions. Their charging behavior is characterized by the fact that ionizable amine groups are rather far apart and thus ionize almost independently. Since the primary amine groups at the exterior are more basic than the tertiary amine in the core, the primary amines protonate already around pH 10, while the tertiary amines around pH 7. For pH values below 5, the dendrimers are fully protonated. The bare charge of G10 dendrimer is about 8000 charges, but even at pH 10 there will be still about 2000.
Charged dendrimers interact strongly in solution due to electrostatic repulsion [1,2]. The interaction potential u(r), which depends on the center-to-center distance r, is well approximated by the screened Coulomb potential
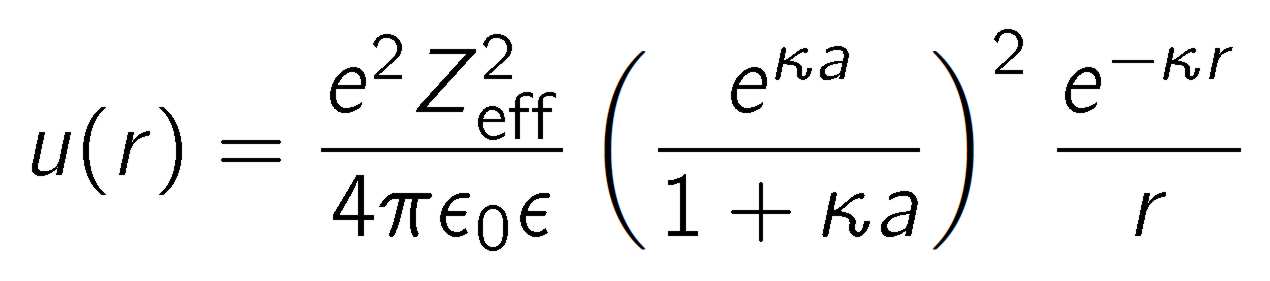
where Zeff is the effective charge of the dendrimer in units of the elementary charge e, ε0 the permittivity of vacuum, ε the dielectric constant, and κ-1 is the Debye length. The latter is given by
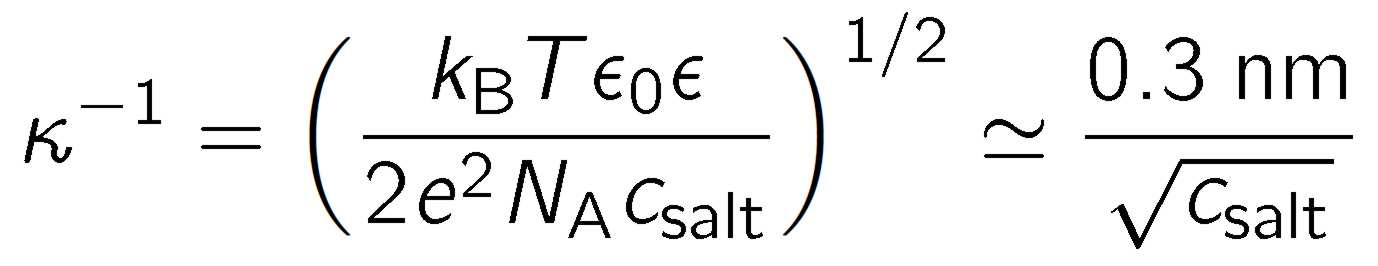
where csalt is the concentration of added monovalent salt expressed in mol/L, NA is the Avogadro's number, kB Boltzmann's constant, and T the absolute temperature. The approximate numerical relation applies in water at room temperature. Neutron scattering experiments reveal that the effective charge of dendrimers is much smaller than the bare charge. For highly charged objects, the effective charge can be approximated by the saturation value obtained from Poisson-Boltzmann theory
![]()
where LB = e2/(4πε0εkBT) is the Bjerrum length. In water at room temperature LB is about 0.72 nm. Based on the above equation ones expects that the effective charges of PAMAM dendrimers are well below 100. The same conclusion was also reached from neutron scattering experiments [1,2].
Adsorption kinetics
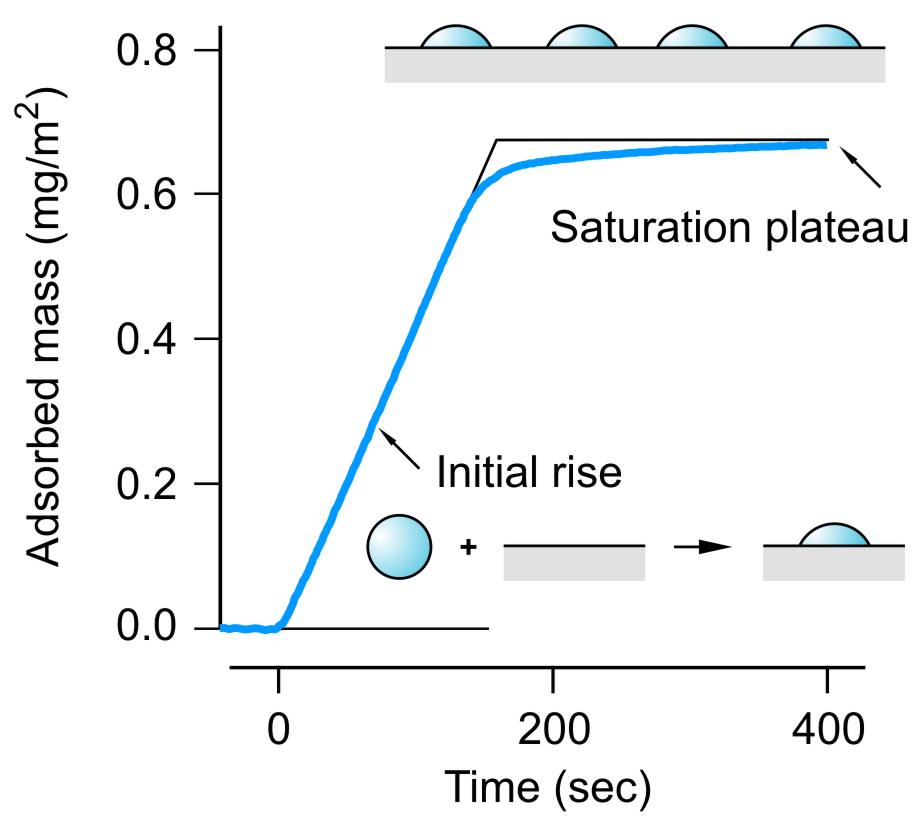 Adsorption of dendrimers from aqueous solutions to an oppositely charged substrates can be easily studied by reflectivity with silica [4]. Reflectivity is a optical surface sensitive technique based on the analysis of the polarization the reflected light, and yields the adsorbed mass in real time. A typical adsorption trace of PAMAM G10 dendrimers of the adsorbed amount Γ
versus time t is shown in the right figure. The substrate is first flushed with a dendrimer-free solution of monovalent electrolyte, and then starting with t = 0 a dendrimer solution of 1.0 mg/L in the same electrolyte is used. Initially, one observes a linear rise of the adsorbed amount with time. After a while, the adsorption reaches a plateau, indicating the formation of a saturated dendrimer layer. The initial regime is dominated by adsorption of single dendrimers on the surface, and therefore the adsorption rate can be modeled by a first order rate process
Adsorption of dendrimers from aqueous solutions to an oppositely charged substrates can be easily studied by reflectivity with silica [4]. Reflectivity is a optical surface sensitive technique based on the analysis of the polarization the reflected light, and yields the adsorbed mass in real time. A typical adsorption trace of PAMAM G10 dendrimers of the adsorbed amount Γ
versus time t is shown in the right figure. The substrate is first flushed with a dendrimer-free solution of monovalent electrolyte, and then starting with t = 0 a dendrimer solution of 1.0 mg/L in the same electrolyte is used. Initially, one observes a linear rise of the adsorbed amount with time. After a while, the adsorption reaches a plateau, indicating the formation of a saturated dendrimer layer. The initial regime is dominated by adsorption of single dendrimers on the surface, and therefore the adsorption rate can be modeled by a first order rate process
![]()
where kads is the adsorption rate coefficient, and cden the concentration of dendrimers in solution. By varying the dendrimer concentration one can demonstrate that the adsorption process is indeed of first order in the dendrimer concentration, and one finds a rate coefficient of about 3.5 μm/s. This value compares rather well with the transport limited adsorption rate coefficient of 5.0 μm/s deduced theoretically from the cell geometry. The reason that lower values are observed experimentally is probably due to the neglect of van der Waals and hydrodynamic interactions in the transport limited adsorption model.
Saturated layer
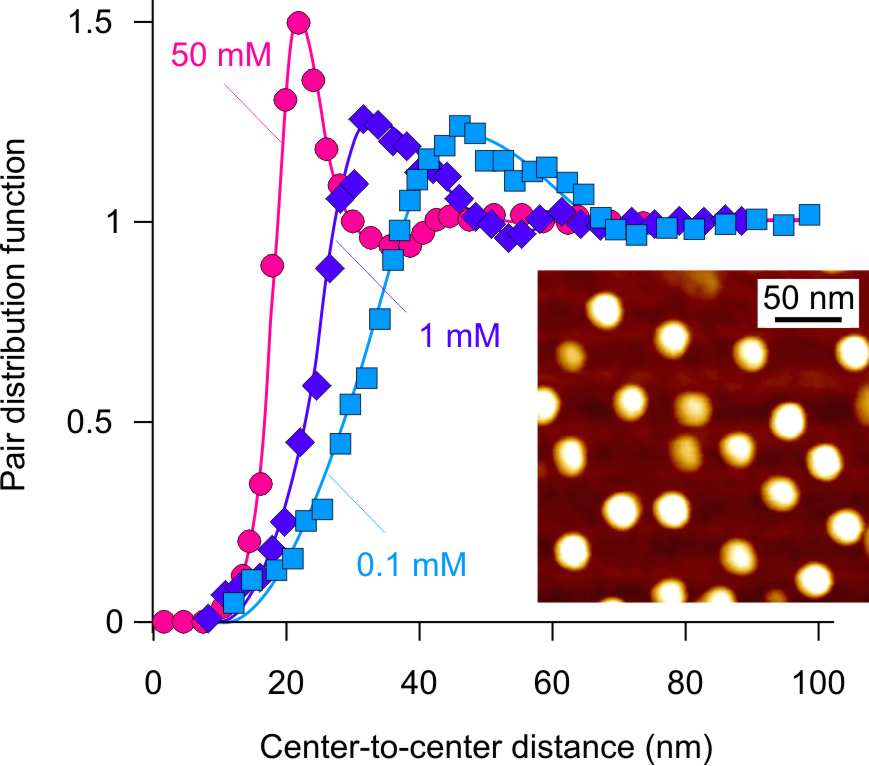
The saturation plateau is determined by blocking of the surface by the adsorbing dendrimers. Due to the low adsorbed amount, one deals with loose monolayers. The strong attractive forces between the dendrimers and the oppositely charged substrate suggest that the adsorption of dendrimers follows the random sequential adsorption (RSA) model. This model assumes that an object that approaches the surface from solution adsorbs irreversibly. However, this object will not adsorb when it is obstructed with an another object already adsorbed. This model predicts saturation of the surface at a finite coverage, so-called jamming limit. For hard circular disks placed on a planar surface, the jamming limit θjam is attained at a coverage of about 0.55.
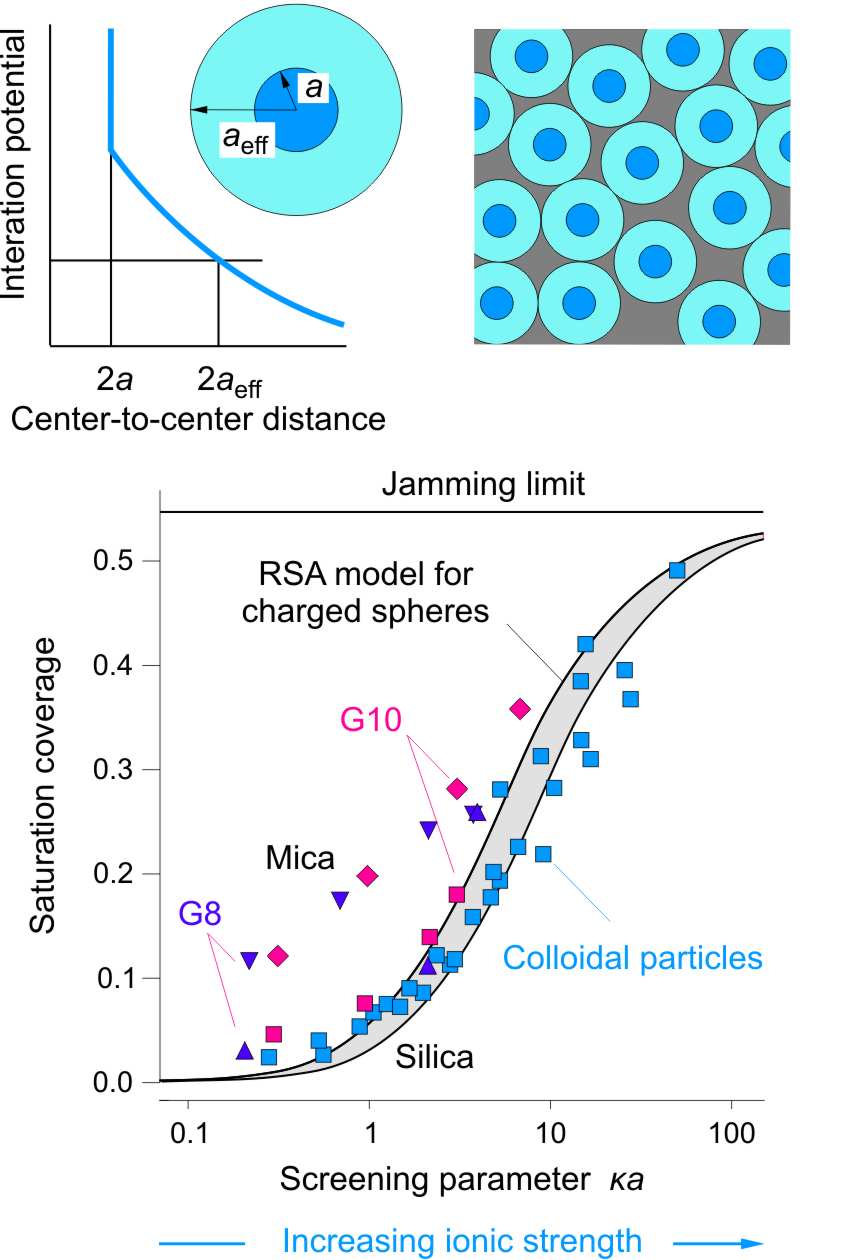 The right figure reports the surface coverage at the adsorption plateau as a function of the screening parameter κa. This representation compares the adsorption of dendrimers at pH 4 with the deposition of larger charged colloidal particles to oppositely charged substrates [5,6]. One observes that dendrimers behave rather similarly to colloidal particles. At high ionic strength, the coverage agrees relatively well with the RSA jamming coverage, but at lower ionic strengths the coverage can be much lower. This decrease can be explained by the repulsive screened Coulomb interaction between the dendrimers. In this case, the distance of closest approach will be dictated by the fact that the interaction energy remain comparable to the thermal energy [6]. Therefore, the closest approach of the adsorbing dendrimers will be given by an effective radius aeff whose value is determined by the condition u(aeff) ≅ kBT. The difference between the actual radius and the effective radius is illustrated the left figure on the top. The coverage can be then obtained from
The right figure reports the surface coverage at the adsorption plateau as a function of the screening parameter κa. This representation compares the adsorption of dendrimers at pH 4 with the deposition of larger charged colloidal particles to oppositely charged substrates [5,6]. One observes that dendrimers behave rather similarly to colloidal particles. At high ionic strength, the coverage agrees relatively well with the RSA jamming coverage, but at lower ionic strengths the coverage can be much lower. This decrease can be explained by the repulsive screened Coulomb interaction between the dendrimers. In this case, the distance of closest approach will be dictated by the fact that the interaction energy remain comparable to the thermal energy [6]. Therefore, the closest approach of the adsorbing dendrimers will be given by an effective radius aeff whose value is determined by the condition u(aeff) ≅ kBT. The difference between the actual radius and the effective radius is illustrated the left figure on the top. The coverage can be then obtained from
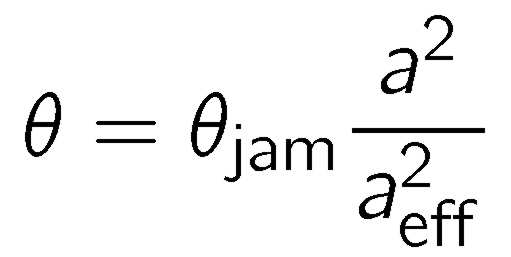
When one assumes that this interaction is well described by the screened Coulomb potential quoted above, one obtains the solid lines shown in the left figure. The grey area reflects the spread of the predictions for the different radii used. The low coverage at low ionic strength can be thus seen as resulting from the electric double-layer repulsion between the highly charged dendrimers. The data for the adsorption on silica agree rather well with the model, while the data for mica leads to substantially higher coverage. This disagreement is related to the higher charge of mica with respect of silica, and this effect be discussed in the following.
 The RSA model discussed so far applied only to weakly charged substrates. In some cases, one observes larger coverage at low ionic strengths, as illustrated for mica in the figure above. The graph in the figure on the right shows that this effect can be very pronounced for dendrimer absorbtion on silica at higher pH. The RSA model discussed above including the electrostatic screened Coulomb interactions between the two dendrimers only describes the data at pH 4. This classical model ignores the role of the substrate. One can include electrostatic interactions induced by the charged substrate, and this extended model describes the experimental data very well when the pH dependent charge of silica is taken into account. The water-silica interface is neutral in acidic conditions, and it develops a substantial negative charge in basic solutions [7].
The RSA model discussed so far applied only to weakly charged substrates. In some cases, one observes larger coverage at low ionic strengths, as illustrated for mica in the figure above. The graph in the figure on the right shows that this effect can be very pronounced for dendrimer absorbtion on silica at higher pH. The RSA model discussed above including the electrostatic screened Coulomb interactions between the two dendrimers only describes the data at pH 4. This classical model ignores the role of the substrate. One can include electrostatic interactions induced by the charged substrate, and this extended model describes the experimental data very well when the pH dependent charge of silica is taken into account. The water-silica interface is neutral in acidic conditions, and it develops a substantial negative charge in basic solutions [7].
The weakening of the repulsions between the dendrimers by the presence of the charged substrate can be explained qualitatively as illustrated in top scheme of the figure on the right. The screened Coulomb interactions between the dendrimers are not strongly modified by the presence of a weakly charged surface. However, a highly charged surface will develop a diffuse layer accumulate counterions, and this layer will increase the concentration of the counterions near the surface. These counterions will provide an additional screening of the electrostatic repulsion between the dendrimers and thus lead to a weaker repulsion between them. This weakened repulsion will induce a smaller effective radius, and thus a higher coverage.
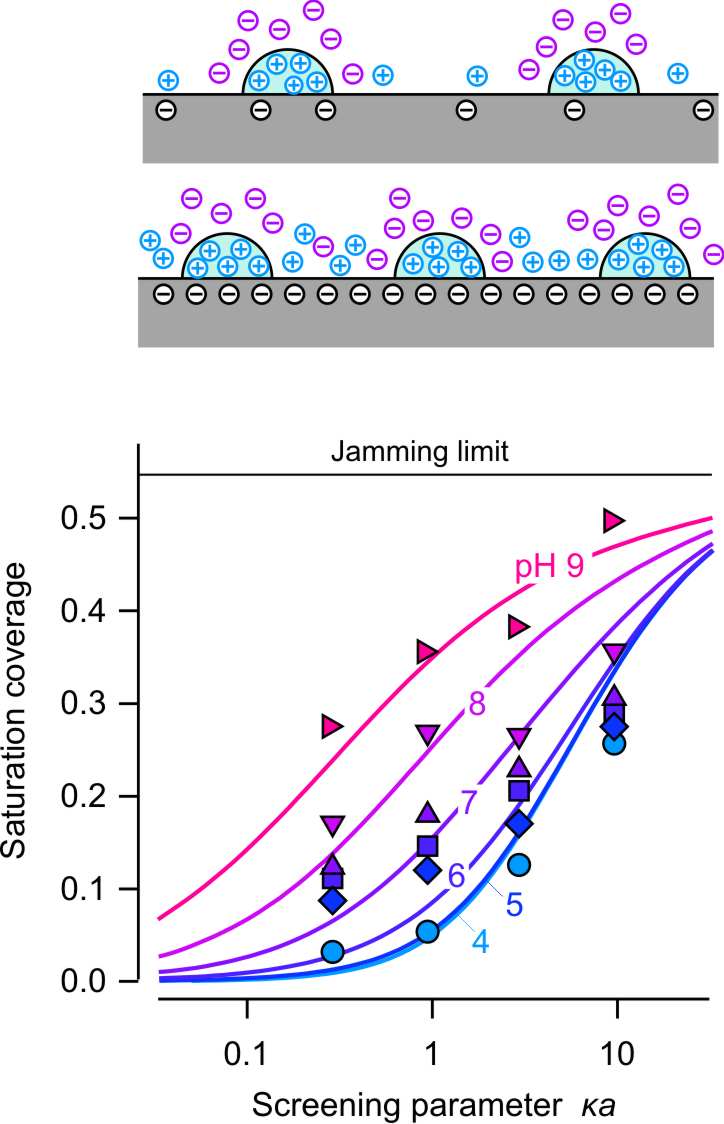
 The fact that adsorbed dendrimers are indeed dilute monolayers can be most clearly revealed by atomic force microscopy (AFM). A typical image of adsorbed G10 dendrimers at low ionic strength is shown as an inset of the figure on the left. The dendrimers cover the surface only partially, and the nearest neighbors assume a certain minimal distance. The monolayer film is actually structured similarly to a liquid as illustrated by the peak in the pair distribution function shown in the figure on the left. The pair distribution function represents the relative concentration of dendrimers around another dendrimer as a function of the center-to-center distance. The position of the peak indicates that there is a characteristic nearest-neighbor distance. This distance decreases with increasing ionic strength since the surface coverage increases as well. This structural peak in the pair correlation function is another important indication that screened Coulomb interactions between the dendrimers are responsible for the saturation of the surface at rather low surface coverage. Similar, but less developed liquid-like structures have been reported for deposited colloidal particles [6].
The fact that adsorbed dendrimers are indeed dilute monolayers can be most clearly revealed by atomic force microscopy (AFM). A typical image of adsorbed G10 dendrimers at low ionic strength is shown as an inset of the figure on the left. The dendrimers cover the surface only partially, and the nearest neighbors assume a certain minimal distance. The monolayer film is actually structured similarly to a liquid as illustrated by the peak in the pair distribution function shown in the figure on the left. The pair distribution function represents the relative concentration of dendrimers around another dendrimer as a function of the center-to-center distance. The position of the peak indicates that there is a characteristic nearest-neighbor distance. This distance decreases with increasing ionic strength since the surface coverage increases as well. This structural peak in the pair correlation function is another important indication that screened Coulomb interactions between the dendrimers are responsible for the saturation of the surface at rather low surface coverage. Similar, but less developed liquid-like structures have been reported for deposited colloidal particles [6].
Desorption and swelling
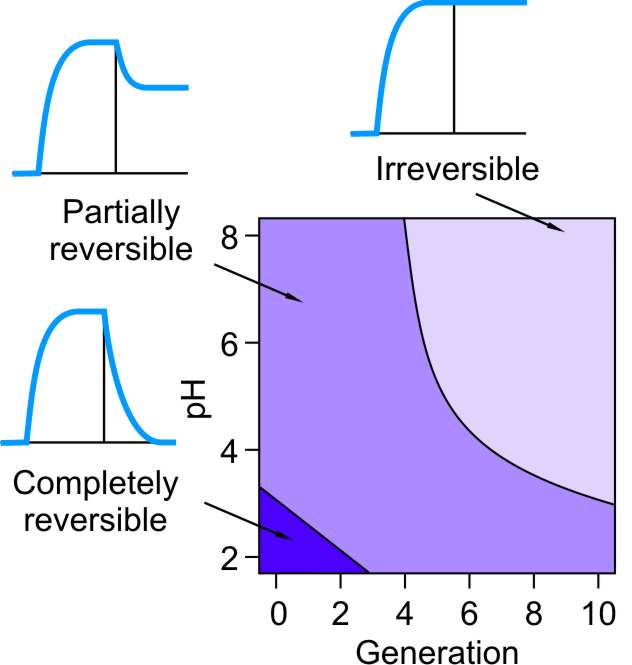 Dendrimers of higher generations adsorbed to silica surfaces cannot be desorbed in pure electrolyte solutions, and therefore the adsorption is basically irreversible. However, dendrimers of lower generation may desorb more or less readily [8]. Three regimes in the dendrimer desorption can be identified, see schemes in the right figure, namely, completely reversible, partially reversible, and irreversible. In the completely reversible regime, the adsorbed film will desorb completely and quickly. In the partially reversible regime, one part of the dendrimers will desorb quickly, while another part will remain adsorbed. In the irreversible regime, desorption cannot be observed within the experimental window covering few hours. The right figure shows a map of these regimes depending on the dendrimer generation and solution pH in 0.1 M KCl electrolyte. The desorption is irreversible for high generation dendrimers and in basic solutions. The desorption is fully reversible for the lowest generations and in very acidic solutions. One encounters the partially reversible regime in between.
This behavior can be interpreted in terms of attractive electrostatic interactions between the positively charged dendrimers and the negatively charged substrate. These interactions become stronger with increasing dendrimer size, which explains the trend towards irreversibility with increasing generation. The charge of the water-silica interface increases strongly in magnitude with pH [7]. The dendrimers are thus strongly attracted to the surface at high pH, while the attraction is weaker at low pH. The observation was also made that increasing the salt concentration the irreversible region shrinks, while the reversible one grows. This trend can be also understood since addition of salt weakens the electrostatic attraction by screening.
Dendrimers of higher generations adsorbed to silica surfaces cannot be desorbed in pure electrolyte solutions, and therefore the adsorption is basically irreversible. However, dendrimers of lower generation may desorb more or less readily [8]. Three regimes in the dendrimer desorption can be identified, see schemes in the right figure, namely, completely reversible, partially reversible, and irreversible. In the completely reversible regime, the adsorbed film will desorb completely and quickly. In the partially reversible regime, one part of the dendrimers will desorb quickly, while another part will remain adsorbed. In the irreversible regime, desorption cannot be observed within the experimental window covering few hours. The right figure shows a map of these regimes depending on the dendrimer generation and solution pH in 0.1 M KCl electrolyte. The desorption is irreversible for high generation dendrimers and in basic solutions. The desorption is fully reversible for the lowest generations and in very acidic solutions. One encounters the partially reversible regime in between.
This behavior can be interpreted in terms of attractive electrostatic interactions between the positively charged dendrimers and the negatively charged substrate. These interactions become stronger with increasing dendrimer size, which explains the trend towards irreversibility with increasing generation. The charge of the water-silica interface increases strongly in magnitude with pH [7]. The dendrimers are thus strongly attracted to the surface at high pH, while the attraction is weaker at low pH. The observation was also made that increasing the salt concentration the irreversible region shrinks, while the reversible one grows. This trend can be also understood since addition of salt weakens the electrostatic attraction by screening.
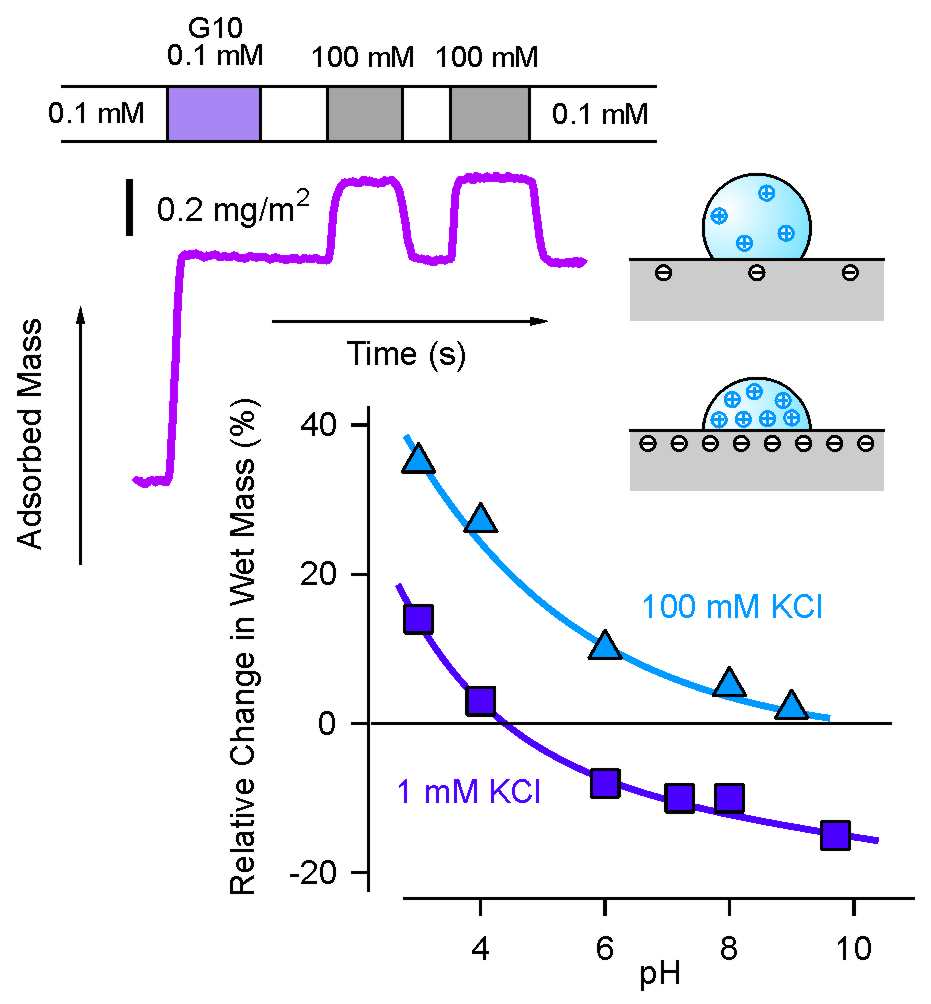 Attractive electrostatic interactions between the dendrimers and the substrate also explain swelling of the dendrimers upon changes with salt and pH. Swelling effects can be best probed by quartz crystal microbalance (QCM) [9]. This technique allow highly accurate mass determinations based measurements of small resonance frequency shifts of a piezoelectric crystal. Since one measures the total mass, the technique is sensitive to the presence of trapped water within the dendrimers. A typical experimental run with G10 dendrimers at pH 4 is shown in the top panel of the left figure. The substrate is flushed with 0.1 mM electrolyte solution, and dendrimers are adsorbed from the same electrolyte. The adsorbed layer is flushed with pure electrolyte solution, which confirms that the layer is irreversibly adsorbed. When the layer is then incubated with a 100 mM electrolyte solution, an increase in mass of about 30% is observed. This increase is due to swelling of the dendrimers. Repeated flushing shows that the swelling process is fully reversible. The lower graph in the left figure illustrates that the extent of the swelling depends strongly on pH. The lower the pH, the stronger the swelling. When the incubating solution is of low salt concentration, the swelling is much weaker, but the same pH dependence is observed. Electrostatic attraction between dendrimers and substrate weakens with decreasing pH and increasing salt level, and therefore the dendrimers swell. Not surprisingly, the same forces that lead to desorption of dendrimers also promote their swelling.
Attractive electrostatic interactions between the dendrimers and the substrate also explain swelling of the dendrimers upon changes with salt and pH. Swelling effects can be best probed by quartz crystal microbalance (QCM) [9]. This technique allow highly accurate mass determinations based measurements of small resonance frequency shifts of a piezoelectric crystal. Since one measures the total mass, the technique is sensitive to the presence of trapped water within the dendrimers. A typical experimental run with G10 dendrimers at pH 4 is shown in the top panel of the left figure. The substrate is flushed with 0.1 mM electrolyte solution, and dendrimers are adsorbed from the same electrolyte. The adsorbed layer is flushed with pure electrolyte solution, which confirms that the layer is irreversibly adsorbed. When the layer is then incubated with a 100 mM electrolyte solution, an increase in mass of about 30% is observed. This increase is due to swelling of the dendrimers. Repeated flushing shows that the swelling process is fully reversible. The lower graph in the left figure illustrates that the extent of the swelling depends strongly on pH. The lower the pH, the stronger the swelling. When the incubating solution is of low salt concentration, the swelling is much weaker, but the same pH dependence is observed. Electrostatic attraction between dendrimers and substrate weakens with decreasing pH and increasing salt level, and therefore the dendrimers swell. Not surprisingly, the same forces that lead to desorption of dendrimers also promote their swelling.
Comparison with the adsorbed dendrimer mass obtained from reflectometry, which is only sensitive to the mass of the bare dendrimers without trapped water, permits to estimate the water content of the dendrimers. Depending on the swelling degree, one finds a water content of about 50-70%. This value is well comparable to the water content of dissolved dendrimers as discussed above. These results are also consistent with volume estimates of the dendrimers by AFM, even though these measurements are less reliable [9,10]. AFM has also been used to estimate the height of adsorbed dendrimers on planar substrates. Dendrimers flatten on planar substrates in the dry state substantially, but when imaged in a liquid their height seems to be much larger. Nevertheless, the interactions between the dendrimer and the substrate determines the conformation of the adsorbed dendrimers. This point was also demonstrated by computer simulations [10].
Conclusion and outlook
We have good understanding how dendrimers adsorb to oppositely charged substrates. The adsorption kinetics is rapid and quickly leads to loose monolayers of low coverage featuring a liquid-like structure. This structure originates from screened Coulomb repulsions between the charge dendrimers, which can be tuned by addition of salt but also through the charge of the substrate. The adsorbed layers are normally irreversibly adsorbed, but desorption may occur for dendrimers of lower generation, especially under acidic and high salt conditions. The desorption is triggered by weakening of attractive electrostatic forces between the dendrimers and the oppositely charged substrate. These forces are also responsible for flattening of the adsorbed dendrimers and their swelling on the surface. Adsorbed dendrimers may swell substantially, especially in acidic and high salt conditions.
Adsorbed dendrimers films could have interesting applications in material science. The loose liquid-like structures could be useful for surface patterning. Colloidal lithography used similarly structured particular films as masks [11], but dendrimers do offer the possibility to create patterns truly on the nanoscale. Another interesting application might be the swelling response of adsorbed dendrimers. The reversible nature of the swelling process of adsorbed dendrimers could be used as an alternative scheme for drug or gene delivery.
Michal Borkovec
Email. Michal.Borkovec@unige.ch
Direct link www.colloid.ch/dendrimers
First posted, July 31, 2012, last revision, February 16, 2015
This work is licensed under a Creative Commons Attribution 4.0 International License.
References
[1] Ballauff M., Likos C. N. (2004) Dendrimers in solution: Insight from theory and simulation. Angew. Chem. Int. Edit. 43, 2998-3020, 10.1002/anie.200300602.
[2] Porcar L., Liu Y., Verduzco R., Hong, K. L., Butler P. D., Magid L. J., Smith G. S., Chen W. R. (2008) Structural investigation of PAMAM dendrimers in aqueous solutions using small-angle neutron scattering: Effect of generation, J. Phys. Chem. B 2008, 112, 14772-14778, 10.1021/jp805297a.[3] Cakara D., Kleimann J., Borkovec M. (2003) Microscopic protonation equilibra of poly(amidoamine) dendrimers from macroscopic titrations, Macromolecules 36, 4201-4207, 10.1021/ma0300241.
[4] Cahill B. P., Papastavrou G., Koper G. J. M., Borkovec M. (2008) Adsorption of poly(amido amine) (PAMAM) dendrimers on silica: Importance of electrostatic three-body attraction, Langmuir, 24, 465-473, 10.1021/la7021352.
[5] Bohmer M. R., van der Zeeuw E. A., Koper, G. J. M. (1998) Kinetics of particle adsorption in stagnation point flow studied by optical reflectometry, J. Colloid Interface Sci. 197, 242-250, 10.1006/jcis.1997.5236.
[6] Adamczyk Z., Warszynski P. (1996) Role of electrostatic interactions in particle adsorption, Adv. Colloid Interface Sci. 1996, 63, 41-149, 10.1016/0001-8686(95)00281-2.
[7] Kobayashi M., Skarba M., Galletto P., Cakara D., Borkovec M. (2005) Effects of heat treatment on the aggregation and charging of Stöber-type silica, J. Colloid Interf. Sci. 292, 139-147, 10.1016/j.jcis.2005.05.093.
[8] Longtin R., Maroni P., Borkovec M. (2009) Transition from completely reversible to irreversible adsorption of poly(amido amine) dendrimers on silica, Langmuir, 25, 2928-2934, 10.1021/la8038818.
[9] Muresan L., Maroni P., Popa I., Porus M., Longtin R., Papastavrou G., Borkovec M. (2011) Conformational changes of polyamidoamine (PAMAM) dendrimers adsorbed on silica substrates, Macromolecules 44, 5069-5071, 10.1021/ma201103n.
[10] Mecke A., Lee I., Baker J. R., Holl M. M. B., Orr B. G. (2004) Deformability of poly(amidoamine) dendrimers, Eur. Phys. J. E 2004, 14, 7-16, 10.1140/epje/i2003-10087-5.
[11] Michel R., Reviakine I., Sutherland D. S., Fokas G., Csucs G., Danuser G., Spencer N. D., Textor, M. (2002) A novel approach to produce biologically relevant chemical patterns at the nanometer scale: Selective molecular assembly patterning combined with colloidal lithography, Langmuir 2002, 18, 8580-8586, 10.1021/la0258244.
