Derjaguin, Landau, Vervey, and Overbeek (DLVO) developed a theory of colloidal stability, which currently represents the cornerstone of our understanding of interactions between colloidal particles and their aggregation behavior. This theory is also being used to rationalize forces acting between interfaces and to interpret particle deposition to planar substrates. The same theory is also used to rationalize forces between planar substrates, for example, thin liquid films.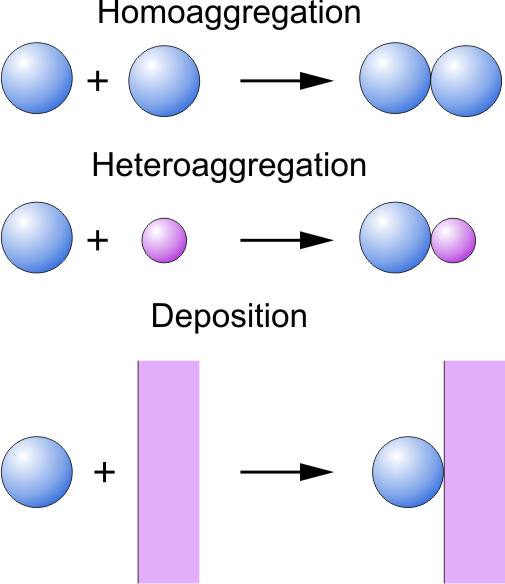 
The principal ideas were first developed by Boris Derjaguin [1], then extended in a landmark article jointly with Lev Landau [2], and later more widely publicized in a book by Evert Verwey and Jan Overbeek [3]. The theory was initially formulated for two identical interfaces (symmetric system), which corresponds to the case of the aggregation of identical particles (homoaggregation). This concept was later extended to the two different interfaces (asymmetric system) and aggregation of different particles (heteroaggregation). In the limiting case of large size disparity between the particles, this process is analogous to deposition of particles to a planar substrate. These processes are illustrated in the right figure. The present essay provides a short summary of the relevant concepts, for more detailed treatment the reader is referred to textbooks [4-6].
The force F(h) acting between two colloidal particles having a surface separation h can be related to the free energy of two plates W(h) per unit area by means of the Derjaguin approximation [4,5]
where the effective radius is given by
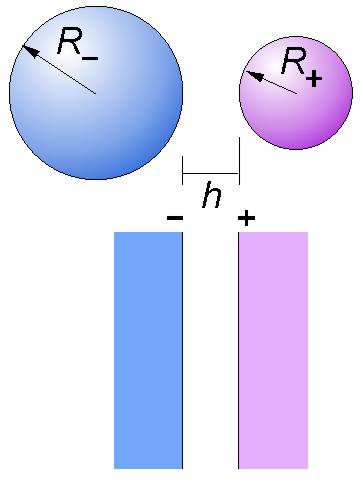where R+ and R– are the radii of the two particles involved as shown in the right figure. In the case of a symmetrical systems where the particles have the same radius R, one has Reff = R/2. This approximation is good when the size of the particles is larger compared to range of the forces involved, which is normally the case in most colloidal systems, except for small nanoparticles. Here the focus is on the interaction between solid substrates across an aqueous electrolyte solution, even though many of the concepts discussed also apply to soft substrates (e.g., fluid films, bubbles) and to other liquids.
When the force between the particles is known, one can calculate the interaction free energy of the two particles by its integration
DLVO theory assumes that the free energy per unit area can be well approximated by two additive contributions, namely
These two contributions refer to van der Waals and double layer interactions. The above equation can be also used to model forces between to planar substrates (e.g., liquid films), and is sometimes also referred to as the DLVO theory. In its original version, however, the DLVO theory includes the additional step to calculate aggregation rates. We adopt this point of view here as well.
Van der Waals forces are almost always present, and they result from interactions of the rotating or fluctuating dipoles of atoms and molecules. In the simplest situation, this interaction can be modeled as
where H is the Hamaker constant, which defines its strength. In most situations, the Hamaker constant is positive, meaning that the van der Waals force is attractive. Typical values of H are 10–21 – 10–19 J. These values may slightly decrease with increasing salt level. The above relation is good at smaller separations for smooth substrates. At larger distances the interaction decays more quickly due to retardation effects, while surface roughness may reduce this interaction at smaller distances.
Double layer interactions are important for charged substrates, especially at lower salt levels. The interaction free energy can be approximated as
where σ+ and σ– are the surface charge densities per unit area of the right and left surface, ε0 is the permittivity of vacuum, ε the dielectric constant of water, and κ is the inverse Debye length. The latter is given by
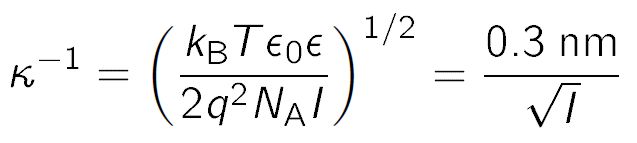
where q is the elementary charge, NA is the Avocadro's number, I is the ionic strength, kB is the Boltzmann constant, and T is the absolute temperature. The second equality is approximatively valid for water at room temperature. The ionic strength of the solution is given by
where zi is the valence of the ion of type i, ci its concentration expressed in mol/L, and i runs over all types of ions in solution. The ionic strength equals to to the concentration of a salt solution containing monovalent ions, while it is larger for salt solutions containing multivalent ions. One may also characterize the substrate by its electric surface potential ψ±, namely
The above formula for the double layer free energy is referred to as the superposition approximation, and is accurate for larger surface separations and low surface charge densities. Within the latter conditions, one can use the Debye-Hückel theory to calculate the interaction energies. For higher charge densities, the Poisson-Boltzmann theory must be used. At larger distances, however, one may replace the actual surface charge density by an effective value, and the simple exponential dependence often remains a good approximation.
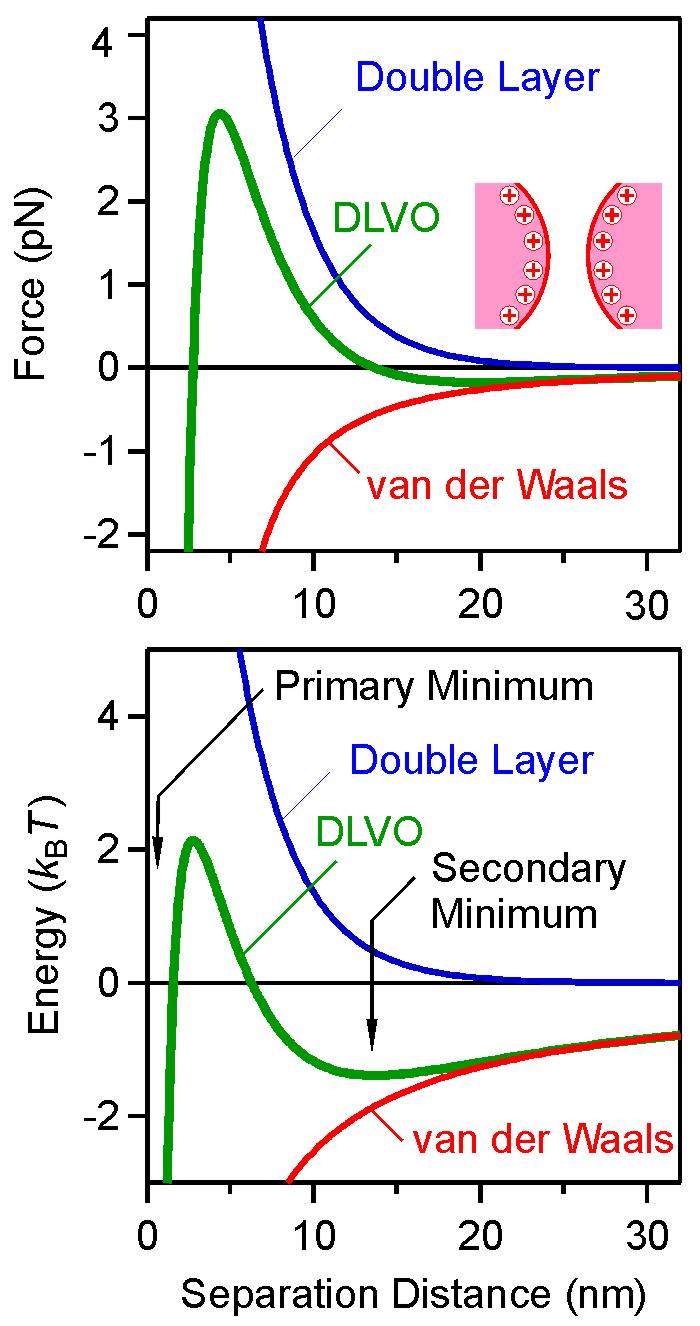
The symmetric situation deals with two identical particles of radius R and a surface charge density σ. Such situations are typically encountered in colloidal suspensions, where all particles are identical, or at least very similar. The figure below shows the force profiles in the left panel, while the potential energy profiles are shown in the right panel. The total DLVO profile is compared with the Van der Waals and double layer contributions. We have used R = 250 nm and a Hamaker constant of H =5.0 × 10–21 J. These parameters will be used in all other examples discussed below. In the figure below, we use a surface charge density σ =2 mC/m2, and a monovalent salt with a concentration of 8 mM. Van der Waals forces dictate the profiles at large and small distances, while the double layer force dominates the intermediate distances.
At contact, the DLVO profile is infinitely deep, but in reality there are repulsive forces acting at very short distances. The combination of these forces with the DLVO force profile results in a deep attractive well, which is referred to as the primary minimum. At larger distances, the energy profile goes then through a maximum, and subsequently passes through a shallow minimum, which referred to as the secondary minimum. Note that when the force vanishes, the energy profile goes through a maximum or a mimimum. In the symmetric situations, the profiles are the same whether the sign of the charge is positive or negative.
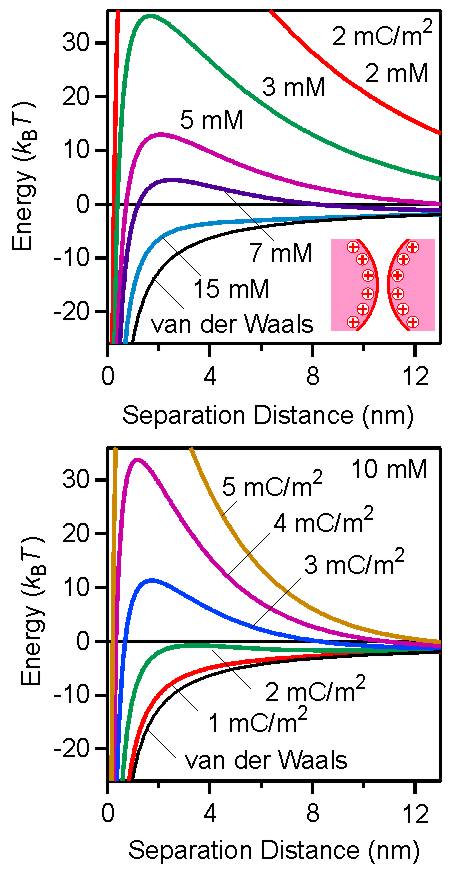
Such DLVO interaction energy profiles evolve in a characteristic fashion, which is illustrated in the left figure. The dependence on the salt concentration is shown in the left panel, while on the surface charge density in the right one. At low salt levels or high surface charge densities, the particles are repulsive, as the interaction is dominated by the double layer contribution. At high salt levels or small surface charge densities, the interaction is dominated by the attractive van der Waals force. At intermediate values, the energy profile passes through a maximum, which occurs at a separation distance that is comparable to the Debye length κ−1. The corresponding force profiles show very similar trends. One should note that such force profiles can be directly measured with various techniques, including the surface forces apparatus (SFA) and the atomic force microscope (AFM) [4,6].
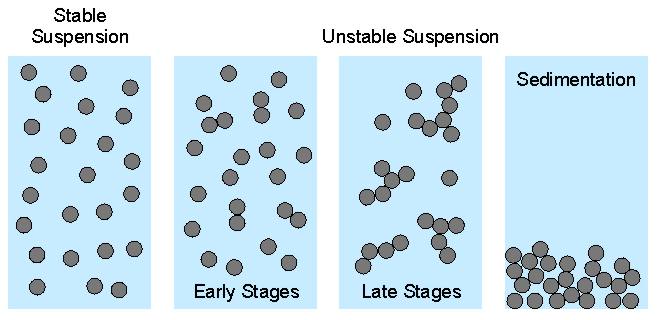When colloidal particles are suspended in water, they will interact according to the energy profiles discussed above. When this profile is strongly repulsive, the particles will repel each other, and form a stable suspension. When this profile is attractive, the particles will approach all the way into contact, and stick to each other. Initially, particle dimers and trimers will form. As the aggregation proceeds, the particles form larger and larger flocs (or clusters, aggregates). As these flocs grow larger, they sediment, and the suspension clarifies. Under these conditions, one says that one has an unstable suspension. When particles aggregate, they are in contact in the deep primary energy minimum. Under some conditions, the particles can be resuspended again. One refers to this reverse process as peptization. But this process hardly occurs spontaneously. The scheme below illustrates these processes.
The suspension stability can be quantified by considering the kinetics of formation of particle dimers, according to the reaction
A + A → A2
where A refers to the individual particle monomer, and A2 to the particle dimer aggregate. The formation of dimers is important in the early stages of the aggregation, while the growth of larger aggregates becomes important as the process continues. When the aggregates become larger, one refers to later stages of the aggregation, but this regime is typically not considered within the DLVO theory. The rate of dimer formation is given by the rate law
where N1 and N2 are the number concentrations of the particle monomers and dimers, t is the time, and k is the aggregation rate coefficient. One uses the same relation in chemical kinetics, except one defines the rate coefficient to be by a factor of two larger. The above equation is used to evaluate the time-dependent concentration of doublets in a suspension initially only composed of monomers of concentration N0, one obtains linear dependencies
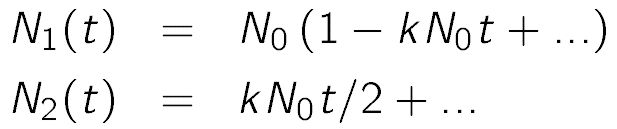
For this reason, one also introduces the characteristic time of aggregation T1/2 = 2/(kN0), whereby the factor of two is introduced such that this characteristic time is identical to the half-time of aggregation in the Smoluchowski's model [4]. This model assumes that aggregates of any size form with the same rate coefficient k. The characteristic time of aggregation is a useful parameter to estimate whether a given suspension is stable within an experimental time window or not. When T1/2 is much larger than the experimental window, the suspension is stable, while when T1/2 is much smaller, the suspension will be unstable. One should note that this characteristic time T1/2 depends on the particle concentration, and thus a dilute suspension is more stable than a concentrated one. The aggregation coefficient can be measured with various experimental techniques, for example, time-resolved light scattering or single particle counting [7,8].
The particles undergo diffusional motion in the suspending fluid, and when they come close enough, they will stick to each other and form an aggregate. However, they also interact with the potential U(h). The aggregation rate due to diffusion in this force-field can be calculated by the Fuchs formula, and the respective expression is also being used in DLVO theory [4,5]
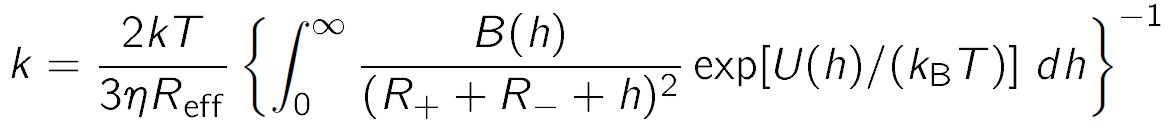
where B(h) is the hydrodynamic resistance function, η is the viscosity of water. The resistance function originates from the hindrance of the diffusion process due hydrodynamic flow created by the second particle, and can be approximated as
This relation reduces to several important special cases. When the particles do not interact, meaning that U(h) = B(h) = 0, one obtains the relation also obtained by Smoluchowski for the diffusion controlled rate [4,5]
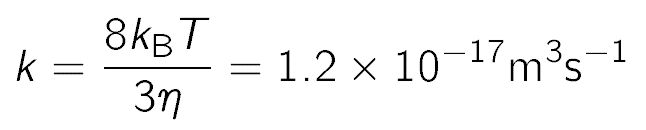
where the numerical value approximately refers to water at room temperature.
At high salt levels, particles aggregate approximately with the diffusion controlled rate, since the van der Waals forces and hydrodynamic interactions have only minor effects. These conditions are also referred to as the fast aggregation or diffusion controlled aggregation. At lower salt levels, and energy barrier develops due to double layer interaction. The aggregation rate is substantially slowed down, since the particles have to cross the barrier by means of thermal motion. This mechanism is similar to a chemical reaction, where the reactants have to cross an activation energy barrier. Therefore, one refers to this regime as slow aggregation or reaction controlled aggregation.
The salt concentration dependencies of the aggregation rate coefficient calculated with the Fuchs expression and the DLVO interaction potential discussed above are shown in the right figure. All curves show the same generic features. At high salt concentration, the aggregation rate is constant, since the aggregation is in the fast regime. When one compares the plateau value calculated by DLVO theory as shown in the figure, one finds that the calculated value is about a factor of 2 lower than the Smoluchowski's value quoted above. This discrepancy originates from the interplay between the van der Waals interaction, which leads to a faster rate, and the hydrodynamic interaction, which leads to a slower rate. A similar effect is observed experimentally [7].
When the salt concentration is decreased, the aggregation rate decreases rapidly due to the presence of the barrier originating from the double layer repulsion. Thereby, one enters the slow regime. One observes that the rate depends sensitively on the salt concentration and also on the surface charge density, as shown in the top panel. The transition between the slow and fast regime is relatively sharp, and therefore referred to as the critical coagulation concentration (CCC). The CCC is an important characteristic of the aggregation process, as it provides a simple stability threshold of a colloidal suspension. As can be seen from the figure above, the CCC decreases with decreasing surface charge density, since the double layer forces also weaken accordingly. For homoaggregation, these dependencies are the same whether the sign of the charge is positive or negative.
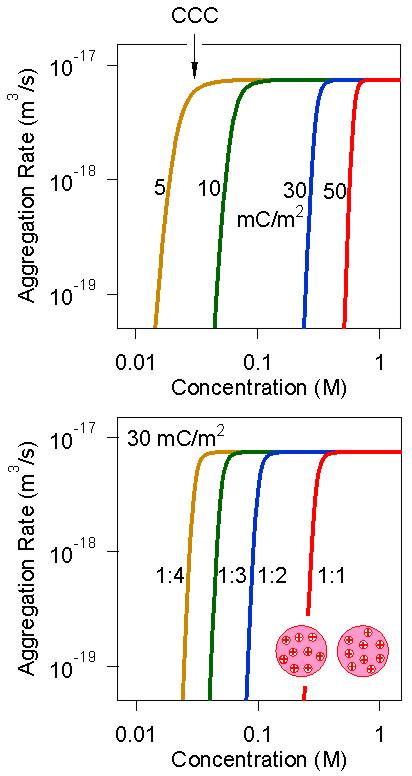
The bottom panel of the figure above shows the salt dependence in different 1:z electrolytes, where the valence of the counterions is being changed. The main influence originates from the fact that the DLVO potential depends on the ionic strength, and in the presence of multivalent ions, the respective concentrations are substantially smaller. The CCC shifts towards smaller concentrations with increasing valence. This shift reflects the classical Schulze-Hardy rule, which states that salts are increasingly more effective in destabilizing colloidal suspensions with increasing valence of the counterions. The actual dependence of the CCC versus the valence is shown in the left figure below. This dependence roughly follows an empirical relation of the type
DLVO theory predicts z = 2 for low surface charge densities for symmetric electrolytes (z:z), while a similar dependence is observed for different asymmetric electrolytes (z:1 or 1:z). This dependence mainly originates from converting the concentration to the ionic strength. For higher charge densities, this dependence becomes more important as shown in the left figure. For unphysically high charge densities, the DLVO theory predicts z = 6 [9].
The secondary minimum normally does not influence the aggregation kinetics. However, for larger particles this minimum can be relatively deep, and in this case the aggregation processes may feature an initial rapid transient. During this transient, the particles aggregate into the secondary minimum. For longer times, the particles overcome the energy barrier and the aggregates transform into those trapped in the primary well [10].
The asymmetric situation deals with two different particles, especially having different surface charge densities σ+ and σ–. Such situations occur in mixtures of colloidal suspensions, or when particles interact with a planar interface. A size disparity between the particles does not introduce any new features, since the two particle radii only enter through the effective radius Reff. For this reason, the interactions in the plate-particle geometry can be also inferred from the same model. When the particles consist of different materials, the actual Hamaker constant might differ, but they normally remain positive. In certain asymmetric situations, however, the van der Waals force can be repulsive, resulting in a negative Hamaker constant. An important example of this type of a setting is a gas bubble interacting with a solid substrate [6]. But here we focus on the common case of attractive van der Waals forces.
Depending on the surface charge densities, the interaction energies may vary widely. Let us illustrate the various types of interactions by discussing two different asymmetric cases, namely the oppositely charged case, and the charged-neutral case. In the oppositely charged chase, the surface charge densities are opposite in sign, but have the same magnitude (σ+ = – σ–). In the charged-neutral case, one of the surfaces is neutral (σ– = 0). The third important case is the symmetric case (σ+ = σ–), and this case was already discussed above. The qualitative features of other situations lie in between these three cases [11].
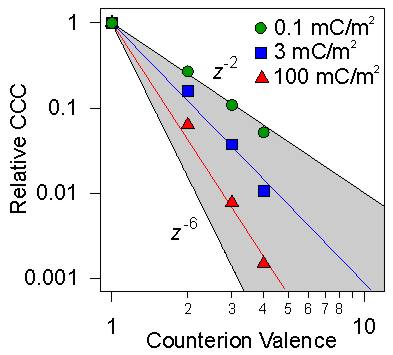
In the oppositely charged case, the forces between particles are always attractive. This feature can be understood, since the double layer force is also attractive and adds to the already attractive van der Waals force. However, the double layer force is strongest at low salt levels, while negligible at high salt. Therefore, the attraction becomes stronger and longer ranged with decreasing salt concentration. This situation is illustrated for the interaction energies in the top panel of the right figure for a charge density of 2 mC/m2. The respective graph for the force profiles would be very similar.
The charged-neutral case is more interesting. Based on the superposition approximation, one would expect that there is no double layer force, when one of the surfaces is neutral. However, the charged surface still has a diffuse layer, and even when a neutral surface is approached, this diffuse layer is compressed, and a net interaction results. This interaction must be treated within the Debye-Hückel model, which is correct for low surface charge densities. At larger distances, the interaction free energy can be shown to behave as [11,12]
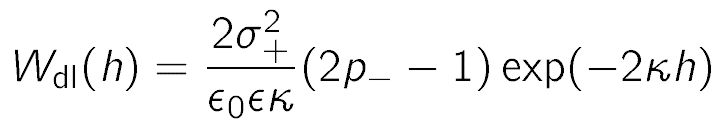
where p– is the regulation parameter of the neutral surface on the left. This parameter characterizes how the surface charge density (or the surface potential) changes upon approach. When the surface charge density remains constant, p– = 1 and one refers to constant charge boundary condition. When the surface potential remains constant, p– = 0, and one refers to constant potential boundary condition. However, this parameter often assumes values between these two limiting situations. For example, the superposition approximation is recovered when p– = 1/2, which refers to intermediate regulation conditions. This charge regulation is related to adsorption of ions to the surface, the extend of which can vary upon approach. The respective interaction energy profiles are shown in the bottom panel of figure above. One observes that depending on the regulation properties of the surface, the interaction can be repulsive or attractive (grey region). Therefore, in the charge neutral case, the charge regulation effects are extremely important. On the other hand, in the symmetric case or the oppositely charged case, charge regulation also plays a role, but the effects are much weaker, and the superposition approximation is relatively accurate.
When a colloidal suspension contains two (or several) types of particles, the aggregation process is much more complicated, since different types of aggregates may contain different types of particles. Consider a suspension that consists two types of particles A and B in the early stages of aggregation. In this situation, we may have two different homoaggregation processes, which lead to two different symmetric particle dimers A2 and B2. Moreover, heteroaggregation may lead to an asymmetric dimer according to the scheme
A + B → AB
In some situations, some of the processes may be very slow, but in others, they can all occur simultaneously. The corresponding rate law for the heteroaggregation process in the early stages reads
where the rate coefficient k can be again calculated by the Fuchs' expression quoted above. We will again discuss the two relevant asymmetric cases, namely the oppositely charged case, and the charged-neutral case.
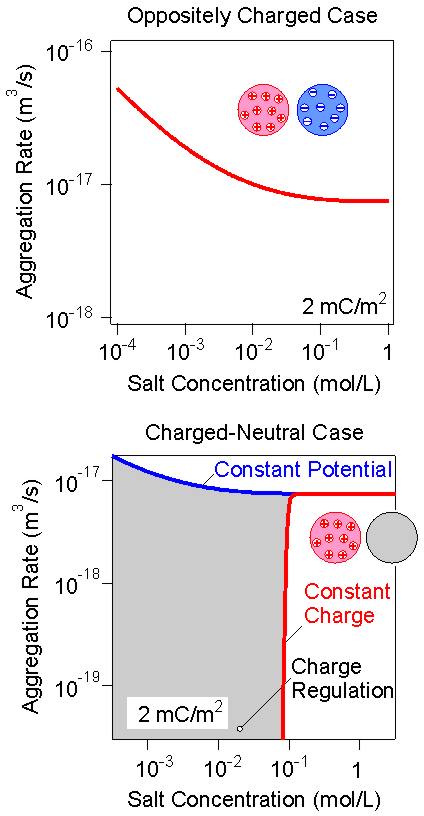In the oppositely charged case, the interaction energies are attractive. The salt dependence of the heteroaggreagtion rate constant is shown in the top panel of the right figure. Since the attraction becomes stronger with decreasing salt level, the aggregation becomes faster, but the effect is relatively weak, as ones notes observing the y-scale of the figure. This effect is weak since the aggregation remains close to diffusion controlled. In the case of homoaggregation, on the other hand, the effect of salt is extremely important, since the potential profile develops a barrier, which substantially slows down the aggregation process.
The aggregation rates in the charged-neutral case as shown in the bottom panel of the right figure features a transition from a situation resembling homoaggregation to situation similar to heteroaggregation in the oppositely charged case. Again, charge regulation effects are extremely important. For constant potential conditions, the interaction energies are attractive. Therefore, the aggregation rate remains close to diffusion controlled, albeit showing a similar minor enhancement as discussed in the oppositely charged case. For constant charge conditions, the interaction energies are repulsive at low salt levels, while they become attractive at high levels. Therefore, the dependence of the aggregation rate is similar to homoaggregation, and also features a CCC. However, this CCC occurs at much lower salt concentrations, since the repulsive forces are weaker. Clearly, effects of charge regulation are again extremely important in this situation. In the presence of multivalent ions, the asymmetric situation remains analogous. The force profiles and aggregation diagrams will be similar when the same ionic strength is being used, the least for sufficiently low charge densities.
The DLVO theory represents an important framework to model interactions in aqueous colloidal suspensions and the respective aggregation rates. The theory assumes that the interaction forces can be well approximated by a superposition of van der Waals and double layer forces. In an symmetric system or in the case of homoaggreagtion, van der Waals forces are attractive and double layer forces repulsive. When one deals with asymmetric systems and heteroaggregation, the situation is can be more complex. While van der Waals forces are normally attractive, the double layer forces can be attractive, repulsive, or both. Moreover, effects of charge regulation can become important. DLVO theory is further capable to describe experimental situations relatively well. In some cases, this theory can describe interaction forces as well as aggregation rate constants quantitatively. Deviations may persist, however, especially at higher salt levels. These details are subject of current research.
Gregor Trefalt and Michal Borkovec
Email. Gregor.Trefalt@unige.ch,
Michal.Borkovec@unige.ch
Direct link www.colloid.ch/dlvo
First posted, September 29, 2014, last revision, November 16, 2017.
This work is licensed under a Creative Commons Attribution 4.0 International License.
[1] Derjaguin, B. (1939) A theory of interaction of particles in presence of electric double-layers and the stability of lyophobe colloids and disperse systems, Acta Phys. Chim., 10, 333-346.
[2] Derjaguin, B. and Landau, L. D. (1941) Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes Acta Phys. Chim., 14, 633-662.
[3] Verwey, E. J. W. and Overbeek, J. T. G. (1948) Theory of Stability of Lyophobic Colloids. Elsevier Amsterdam.
[4] Russel, W. B., Saville, D. A., and Schowalter, W. R. (1989) Colloidal Dispersions. Cambridge University Press Cambridge.
[5] Elimelech, M., Gregory, J., Jia, X., and Williams, R. A. (1995) Particle Deposition and Aggregation: Measurement, Modeling, and Simulation. Butterworth-Heinemann Ltd. Oxford.
[6] Israelachvili, J. (2011) Intermolecular and Surface Forces, 3 ed. Academic Press London.
[7] Holthoff H., Schmitt A., Fernandez-Barbero A., Borkovec M., Cabrerizo-Vilchez M. A., Schurtenberger P., Hidalgo-Alvarez R. (1997) Measurement of absolute coagulation rate constants for colloidal particles: Comparison of single and multiparticle light scattering techniques, J. Colloid Interface Sci., 192, 463-470, Link to publisher.
[8] Trefalt G., Szilagyi I., Borkovec M. (2013) Measuring particle aggregation rates by light scattering, www.colloid.ch/aggregation.
[9] Trefalt G., Szilagyi I., Borkovec M. (2013) Poisson-Boltzmann description of interaction forces and aggregation rates involving charged colloidal particles in asymmetric electrolytes, J. Colloid Interf. Sci. 406, 111-120, 10.1016/j.jcis.2013.05.071.
[10] Behrens S. H., Borkovec M. (2000) Influence of the secondary interaction energy minimum on the early stages of colloidal aggregation, J. Colloid Interface Sci. 225, 460-465. Link to publisher.
[11] Trefalt G., Montes Ruiz-Cabello F. J., Borkovec M. (2014) Interaction forces, heteroaggregation and deposition involving charged colloidal particles, J. Phys. Chem. B 118, 6346-6355, 10.1021/jp503564p.
[12] Carnie S. L., Chan D. Y. C. (1993) Interaction free energy between plates with charge regulation: A linearized model, J. Colloid Interface Sci. 161, 260-264. Link to publisher.